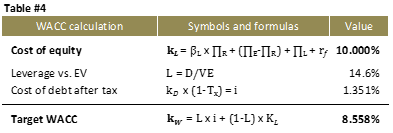A company's valuation is generally derived from several approaches. Assuming that we have an initial idea of a company's equity value, then this value allows us to estimate the "size premium" and thus calculate the discount rate for a DCF model.
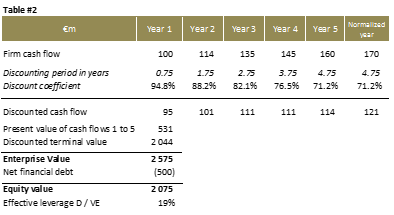
It should be noted that the cash flows are discounted at the end of the financial year, in accordance with the method used to calculate the Fairness Finance risk premium.
As the size premium is a decreasing function of value, the absence of an exogenous equity value implies an iterative approach, obtained by implementing successive iterations until the value retained for the premium and the one resulting from the DCF converge towards a single equity value.

WACC with sector leverage and a prior equity valuation
A company's valuation is generally derived from several approaches : DCF, listed peer comparison, transaction multiples, stock quotes and bloc trades. Assuming that we have an initial idea of a company's equity value using the multiples method, then this value allows us to estimate the "size premium"
[1] and thus calculate the discount rate for a DCF model:
- Imagine that the value of equity indicated by the multiples approach is $2bn. Entering this value in the calculator available on our site leads to a size premium of ΠL, equal to 0.73%;
-
Assuming the company operates in the food, beverage and tobacco sector, the beta with leverage provided on the Fairness Finance site is 0.884;
- Based on the "Enterprise Value"[2],
the sector's debt leverage is 12.1%. In an initial approach, this sector leverage is used to calculate the company's cost of capital, irrespective of its actual debt at the calculation date ($500m) since the latter is supposed to converge toward the sector standard;
- The cost of the corporation's after-tax debt is 1.35% (with the target debt leverage selected);
-
The appraiser's operating cash flow forecasts for the next five years are summarized in Table 2. A growth to infinity rate of 1.5% (the rate the evaluator deems in line with industry practice) is used to calculate the terminal value.
Based on this information, the weighted average cost of capital, or WACC
[3], is 7.420%, as shown in Table 1.
With ΠE designating the “anticipated market risk premium” and ΠR the “CAPM risk premium” provided on our website[4].
As shown in Table 2, the company's equity value stands at $2.075bn.
It should be noted that the cash flows are discounted at the end of the financial year, in accordance with the method used to calculate the Fairness Finance risk premium.
WACC with sector leverage and iterative calculation of the size premium
In the previous example, we used an exogenous equity value of $2bn to calculate the size premium. However, the shareholders' equity value resulting from the DCF is 4% higher, at $2.075bn. Since the size premium is a decreasing function of value, at this stage it is therefore overstated, which penalizes the DCF value.
To remedy this anomaly, an equilibrium value should be calculated to ensure that the value obtained by DCF is equal to the one used for calculating the size premium. This result is obtained by implementing successive iterations until the value retained for the premium and the one resulting from the DCF converge towards a single equity value:
- With a value of $2.310bn, the calculator on our website shows a size premium of 0.65%, which implies a WACC of 6.918%. This discount rate leads to a value of $2.323bn (result of the first iteration);
- By retaining the previous $2.323bn value, the same procedure leads to a WACC of 6.915%, resulting in a discounted value of $2.325bn (2nd iteration);
- Using the previous $2.323bn value, the same procedure leads to a WACC of 6.915%, resulting in a discounted value of $2.325bn (3rd iteration);
- Assuming this value of $2.325bn for the calculation of the size premium, the DCF now points to $2.325bn. This fourth and last iteration leads to an equity value identical to the previous one; the DCF valuation thus converged towards its equilibrium value[5].
The four successive iterations and their respective results are summarized in the following table:
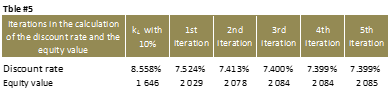
The equilibrium value of the model, i.e. $2.085bn, is thus $10m higher than previously established without iteration.
If no estimate of the equity value is available prior to the calculation of the cost of capital, a surrogate approach is to begin calculations assuming the cost of equity is 10%. In the following example, this approach leads to a WACC of 8.558%
Starting with this discount rate, the DCF shows a $1.646bn equity value. By repeating the iterative procedure described above, in 5 steps, the DCF again converges toward the equilibrium value of $2.085bn, as shown in the following table.
[1] Premium defined in methodological notes n° 3 and n° 4. [2] That is, the sum of the market value of equity and the net amount of financial debt. [3] Weighted average cost of capital. [4] For the definition of these two premia, please see methodological note n° 3. [5] In this case, this method made it possible to determine the equilibrium value of a non-linear 1-order recurrence equation.