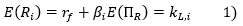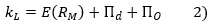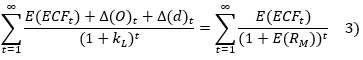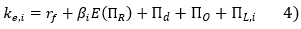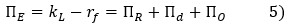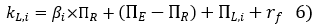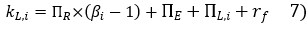Because they are the product of human brains, financial forecasts reflect an optimism bias and therefore are not mathematical expectations in the strict sense of the CAPM.
The gap between the market's implied cost of capital with leverage and the expected return with leverage should be seen as a correction of the forecast cash flows so as to bring them back to mathematical expectations, as required in the CAPM.
The cost of capital of investment grade companies (close to BBB) with reasonably optimistic forecasts, ie a large proportion of listed or likely to be valued companies, can be calculated from the implicit market return if the sector beta is close to 1.
In practice, the cost of capital to be used to discount cash flow to equity is equal to the sum of the the beta adjusted CAPM risk premium, the default risk premium, the risk premium for optimism bias and the the size premium.

The standard capital asset pricing model, CAPM
[1], assumes strict equality between the expected return on the equity market and the expected cost of capital used to discount cash flow forecasts.
where rf is the risk-free rate, E(ΠR) the anticipated market risk premium and βi the beta specific to the stock.
However, because they are produced by human brains, financial forecasts for companies, both internal (management) and external (sell-side analysts) reflect an optimism bias and therefore are not mathematical expectations in the strict sense of the CAPM:
- the forecasts we use are produced by sell-side analysts. Except for very rare exceptions, they assume company survival. They therefore do not take into account the risk of default, which is negligible only for a tiny minority of companies (those with a rating equivalent to AAA). A bond spread is primarily composed of a systematic risk premium (or CAPM premium) adapted to discount the bond's expected cash flow. A default premium that offsets the difference between the contractual debt yield and its expected return is then added to the CAPM risk premium. This default premium depends on a probability of default and a loss given default rate. As a shareholder's recovery rate is close to zero in the event of bankruptcy, the default premium required (Πd) on cash flow assuming survival is greater than that required for a bond.
- the forecast cash flows in case of survival are themselves tainted by an upward bias, all the more marked as the forecast timeline extends far into the future. The existence of this bias is, in our view, well known to investors and analysts themselves. On average, therefore, the cost of capital incorporates a risk premium for optimism bias in conditional cash flows in the case of survival, i.e. ΠO ;
- As the forecast bias is more pronounced for small caps, the sum of Πd and ΠO for these companies is larger, and the difference versus large caps can be aggregated into a size premium, ΠL. It is likely that only a small part of this difference is attributable to a pure liquidity effect.
In other words, the market's implied cost of capital must be greater than its expected return:
The gap between the market's implied cost of capital with leverage, kL , and the expected return with leverage, E(RM) , i.e. the sum of the premia Πd and ΠO, should be seen as a correction of the forecast cash flows so as to bring them back to mathematical expectations, as required in the CAPM.
Thus, the present value of the biased forecasts discounted at the cost of capital must be equal to the value of the mathematical expectations of cash flows discounted at the expected return, E(RM) :
where Δ(O)t and Δ(d)t result respectively from the optimism bias and the lack of probability of default in the cash flow forecasts.
The cost of equity used in the DCF method results from equations 1 and 2:
where E(ΠR) denotes the anticipated market risk premium under the CAPM, Πd + ΠO respectively the default and optimistic bias premia for the total market, and ΠL,i the additional premium that takes into account the size[2] of the individual company "i" .
Note that in equation 4, only βi and ΠL,i are specific to company
"i". This assumes that the default premium and the optimistic bias premium for this company are in our sample's average. This implies an investment grade category (close to BBB) and reasonably optimistic forecasts. In our view, this description defines the majority of companies listed or likely to be valued
[3].
Moreover, as indicated in equation 4, the beta of the evaluated share applies only to the risk premium within the meaning of the CAPM, i.e. to E(ΠR) (which to simplify we will designate by ΠR, or "CAPM risk premium"). The beta defines the systematic risk according to the CAPM and therefore does not apply to the entire gap between the market's implied cost of capital and the risk-free rate.
In what follows, we call "market risk premium" or "total equity spread" the difference between the implied market cost of equity, kL, and the risk-free rate, rf, which we denote by ΠE :
In practice, knowing the market risk premium published by Fairness Finance, ΠE, the CAPM risk premium, ΠR, the size premium and the beta of the security; the cost of capital kL,i to be used to discount cash flow to equity is equal to:
or:
The calculation of a company's cost of equity based on the data computed by Fairness Finance therefore implies the application of equation number 6 or equation number 7
[4].
The ex-ante default and size premia, as well as the CAPM risk premium as we calculate them, are volatile parameters. Estimating these parameters makes it possible to synchronize the cost of capital with the general level of risk aversion at the date of their calculation. The optimism bias premium and the size premium also ensure consistency between the cost of capital and the general level of prices. These parameters avoid the arbitrary use of specific risk premia in addition to the historical risk premium, with the sole aim of ensuring an artificial coherence between the present value resulting from the DCF and the other methods which are also supposed to reflect market value, such as applying the market multiples of comparable listed companies.
[3] For outliers, our offer « pack advanced » will soon give practical solutions.