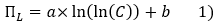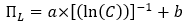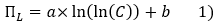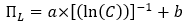La prime de taille - Amérique du Nord à fin 2016
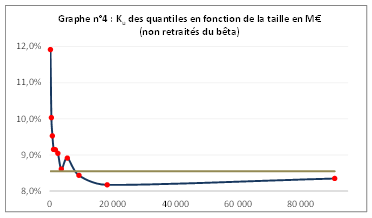
Au 31 décembre 2016, les capitalisations moyennes des 11 quantiles sont comprises entre 160 MUSD (1er portefeuille) et 91 MdsUSD (11e portefeuille). Comme le suggère le graphique n° 4 ci-après, avant neutralisation du risque systématique, les rendements anticipés à dette nulle des 11 portefeuilles suivent, comme en Europe, une fonction décroissante de la capitalisation boursière. Les 8 premiers quantiles (72% des sociétés) ont ainsi un rendement exigé supérieur à celui de l'indice.
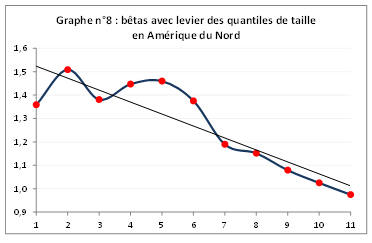
Les 9 premiers quantiles ont des bêtas supérieurs à celui de l'indice (graphique n° 8), contrairement à l'Europe. Une partie du sur-rendement exigé des small caps est donc imputable à leur risque systématique
[8].
Redressés de cet effet de risque systématique, à fin 2016, seuls les 3 premiers quantiles conservent un rendement exigé significativement supérieur à l'indice. Ces trois portefeuilles regroupent les sociétés ayant une capitalisation inférieure à 1 MdUSD, ce qui représente 27 % des sociétés de notre indice.
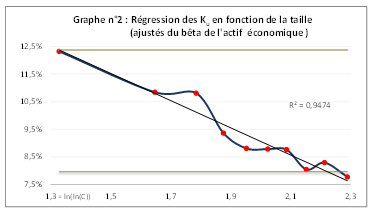
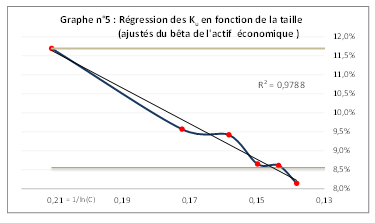
En effectuant un second découpage plus fin sur la base de portefeuilles de 120 sociétés chacun, l'existence d'une prime de taille demeure avérée pour les sociétés de moins de 1 MdUSD. La régression du rendement par rapport à l'inverse du logarithme de la taille (équation ci-après), telle que figurée dans le graphique n° 5, présente un coefficient de détermination r² de 98 %.
La prime de taille pour une société quelconque de moins de 1 MdUSD se calcule ainsi selon la fonction suivante :
Où C désigne la capitalisation boursière de la société évaluée.
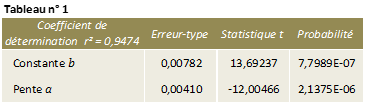
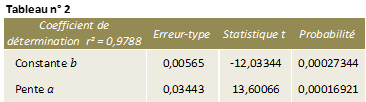
Les données de la régression sont résumées dans le tableau ci-dessous :
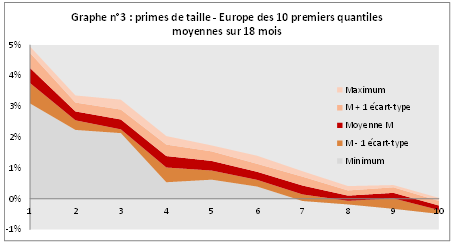
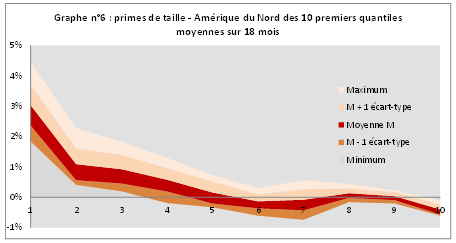
Les moyennes (avant lissage) sur 18 mois et les indicateurs de dispersion des primes de taille des 10 premiers quantiles sur 11 sont représentés dans le graphique ci-après, lequel permet d'identifier l'existence d'une prime de taille entre le 1er et le 4e portefeuille
[9] (soit pour des capitalisations inférieures à 1 MdUSD), avec toutefois des variations d'un mois sur l'autre pouvant conduire à la disparition de la prime à partir du 4e quantile et son apparition jusqu'au 9e.
Conclusion
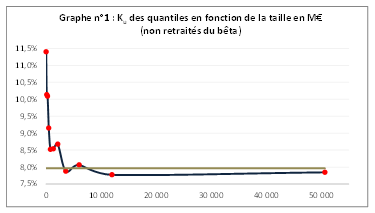
La prime de taille en Europe est décroissante de façon monotone jusqu'au 8e quantile avant lissage au moyen d'une régression. Cette relation établie sur la base des rendements exigés à dette nulle, est avérée, que ces derniers soient ou non retraités du bêta du quantile.
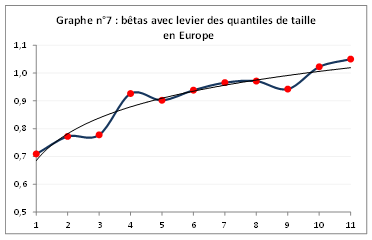
La neutralisation du risque systématique accentue l'effet taille et l'étend à 9 quantiles sur 11, soit pour les sociétés jusqu'à 7,9 Mds€ de capitalisation. Ceci résulte de ce que les bêtas mensuels (avec levier) des 11 portefeuilles sont eux-mêmes croissants et compris entre 0,7 (very small caps) et 1 (very large caps)
[10].
Pour les sociétés nord-américaines l'effet taille est également patent avant la neutralisation du risque systématique. Toutefois, les bêtas des 10 premiers quantiles étant supérieurs à 1, leur retraitement diminue l'effet taille, i.e. la part du sur-rendement non expliquée par le risque systématique.
Après retraitement des bêtas des quantiles, si l'on redécoupe les sociétés de notre échantillon en portefeuilles de 100 titres chacun, le phénomène de prime de taille tend à disparaître au niveau du 4e quantile, soit au dessus de 1 MdUSD de capitalisation.
Différences transatlantiques :
L'effet de la taille sur le coût du capital implicite des sociétés semble donc être un phénomène plus étendu et régulier en Europe qu'en Amérique du Nord :
- en moyenne sur 18 mois, les primes de taille concernent essentiellement les sociétés de moins de 1 MdUSD en Amérique du Nord, alors qu'en Europe elles touchent de façon régulière les sociétés jusqu'à 2,7 Mds € ;
- en Europe, d'un mois sur l'autre, le domaine d'application de la prime de taille varie entre 2,7 Mds€ de capitalisation et 7,9 Mds€. En Amérique du Nord, ce dernier varie entre 1 MdUSD et 7 MdsUSD.