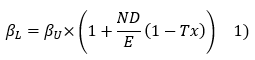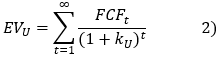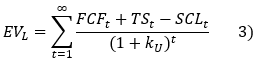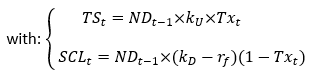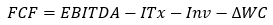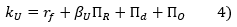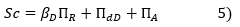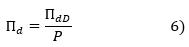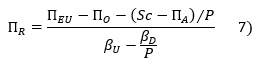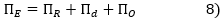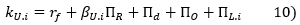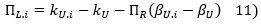The "Adjusted Present Value" approach takes into account leverage, not by correcting the discount rate, but by adjusting cash flow. We use this approach as an intermediate step to calculate the cost of capital with leverage and isolate the risk and size premia.
DCF using an APV approach: definition
Among the many existing formalizations of APV, we retain the equation that in our view seems to be the only one that is consistent with the most widespread model for estimating the impact of leverage on systematic risk, i.e. the Hamada model:
Debt tends to increase the systematic risk of return on equity. Robert Hamada (1972) devised the most common formula used by appraisers for the theoretical link between debt and beta:
Where βL denotes the beta of a company with debt, βU the beta of the same company without financial debt (unlevered), ND the amount of the net financial debt, E the market value of equity, and Tx the deductibility rate of loan interest.
Although this approach has some theoretical limitations, we consider it to be an acceptable approximation of the leverage effect on systematic risk given its simplicity and widespread use (it being specified that default risk is also integrated in our model).
Pablo Fernandez developed the formal interpretation of the Hamada formula in terms of APV. This approach assumes that a company's leverage is managed according to the book value of its assets (cost price and duration of use) and not its equity market value. Using this approach, cash flow adjusted for APV is discounted at the unlevered cost of capital, kU, by deducting the unlevered beta from levered beta, as in equation number 1.
It is therefore equivalent to discounting free cash flow to equity, ECF (equity cash flow), at the cost of equity with leverage, kL, or to discounting at the unlevered cost of capital, kU, an unlevered cash flow, FCF (firm cash flow), adjusted for tax shield, TS, and for the systematic cost of leverage, SCL.
If we assume that the unlevered enterprise value EVU is obtained by the following calculation:
then under the APV approach, the enterprise value with leverage is calculated as follows:
Where ND denotes net debt, Tx the deductibility rate of loan interest, kD the cost of debt and rf the risk-free rate.
As a reminder, unlevered cash flow, FCF (also called operating cash flow) is equal to:
Where EBITDA refers to gross operating income, ITx, corporate income tax, Inv, capital expenditure net of proceeds from the disposal of fixed assets, and ΔWC, the change in working capital.
Inferring the CAPM premium
At the aggregate market level
[1], the unlevered cost of capital is equal to:
where βU means unlevered beta, ΠR, the CAPM risk premium, Πd, the equity risk premium for default, ΠO, the premium for optimism bias, and rf le the risk-free rate[2].
Moreover, the market's average credit spread, SC, is broken down as follows:
where βD denotes the theoretical weighted average beta of corporate bonds in our sample, ΠdD, the default risk premium for corporate bonds and ΠA, the additional premium for AAA-rated corporate bonds compared to government bonds with the same rating and duration.
Using P to denote the creditor-lender loss given default rate, we assume that this is 100% for shareholders:
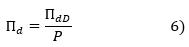
According to equations #1, #4, #5 and #6, we deduce the CAPM risk premium, ΠR :
where ΠEU is the unlevered market risk premium i.e. kU - rf .
This result requires a preliminary estimate of: the credit spread of the companies in our sample; the recovery rate for creditors; the debt betas; and the optimistic bias premium.
Move from market kU to market kL
The levered market risk premium (or "total equity spread"), ΠE, is deduced from the previous results:
Note that the leveraged market risk premium is equal to the difference between the capital cost (with leverage) required on average (weighted by capitalization) and the risk-free rate
[3] :
Deduction of the size premia
With the market's unlevered cost of capital as expressed in equation 4, and kU,i designating one of the size quantiles we use to divide up the companies in our sample:
with ΠL,i denoting the quantile's size premium and βU,i the unlevered beta related to this quantile.
then we deduce the quantile's size premium according to equations #4 and #10:
[1] Average weighted by capitalization. [2] These terms are defined in notes 0, 2 and 3.